Como calcular o erro quadrático médio (MSE) no Microsoft Excel

Nas estatísticas, o erro quadrático médio (MSE) é uma métrica importante que mede a quantidade de erro em um modelo estatístico. Geralmente é usado para avaliar a precisão de um modelo usado para prever valores futuros.

Neste tutorial, explicaremos o que é MSE com mais detalhes e depois mostraremos como calcular MSE no Excel.

O que é erro quadrático médio?

O erro quadrático médio (MSE) é um cálculo que mede a diferença quadrática média entre valores estimados e reais em um conjunto de dados. Em outras palavras, estima a quantidade de erro em um modelo estatístico. Para os geeks de estatística, ele calcula o quão próximo uma linha de regressão se ajusta a um conjunto de pontos de dados.

Por exemplo, digamos que você tenha um modelo que prevê o valor das vendas que você receberá como empresa de software ao longo de um ano. No final do ano, você insere os valores reais de vendas gerados. Você pode então calcular o MSE para ver quão bem seu modelo previu o resultado.

O MSE é calculado calculando a média das diferenças quadradas entre os valores previstos e reais da variável de destino.

A fórmula MSE é semelhante a esta:

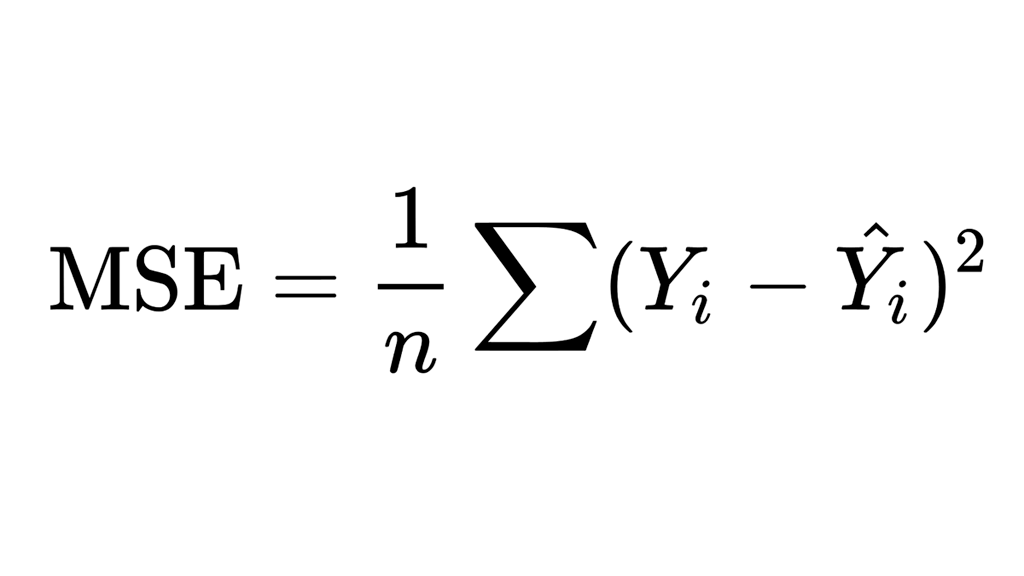
Onde:

Σsignifica a soma dos valores;

né o tamanho da amostra ou número de observações;

Yisão os valores observados e;

Ŷisão os valores previstos.

Um valor de erro mais baixo indica que o modelo tem um erro padrão menor e é melhor na previsão da variável alvo. O MSE é amplamente utilizado em regressão estatística e análise de dados e pode ser útil na comparação de diferentes modelos ou no ajuste de parâmetros para melhorar a precisão das previsões.

Isso parece confuso, mas não é muito difícil de entender quando detalhamos nas seções a seguir.

Como calcular o erro quadrático médio no Microsoft Excel

Existem duas maneiras principais de calcular o MSE no Microsoft Excel: a função SUMSQ, o Função MÉDIA e a fórmula MSE. Usaremos o exemplo abaixo para mostrar como calcular o MSE usando cada uma destas funções:

Neste exemplo simplificado, veremos os valores fictícios de vendas de cada mês (Coluna A). Os valores estimados estão representados na Coluna B e os valores reais na Coluna C..

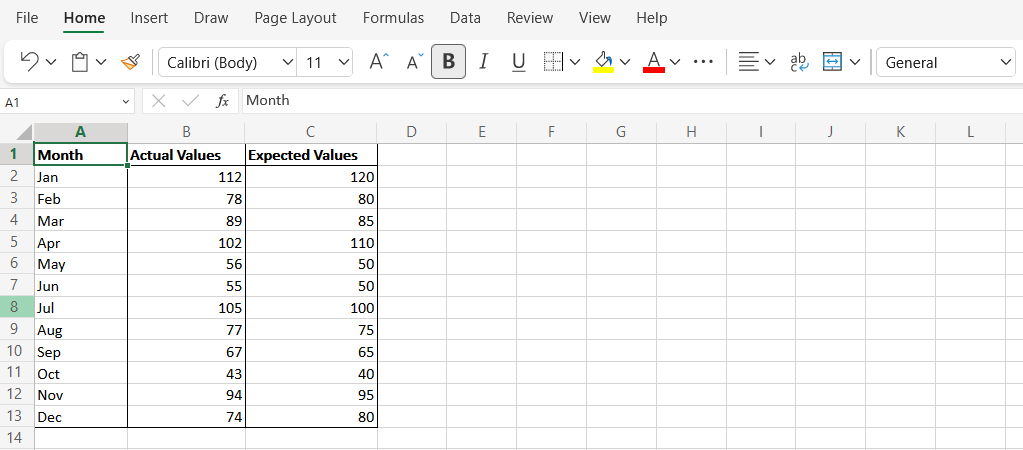
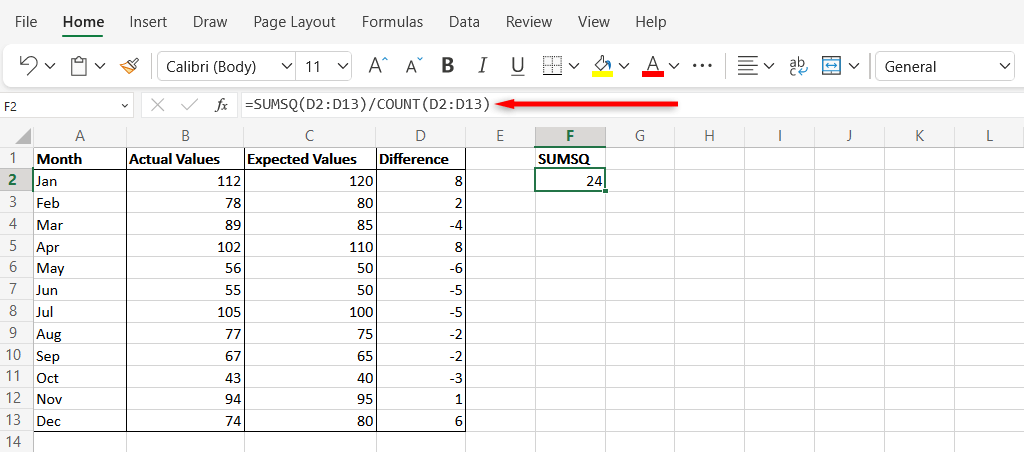
Calcular MSE usando a função SUMSQ

A função SUMSQ no Excel é usada para calcular a soma dos quadrados dos números em um intervalo. Veja como usá-lo para calcular o MSE:

Crie uma nova coluna na Coluna D chamada “Diferença”. Isso representará a diferença entre os valores esperados e reais.

Use a fórmula “C2-B2” para calcular a diferença para os pontos de dados em cada linha.

Selecione uma nova célula e digite a seguinte sintaxe: “=SUMSQ(D2:D13/COUNT(D2:D13)”. Substitua as células na fórmula pelas células corretas da sua planilha do Excel. O resultado final nesta célula é o seu MSE.

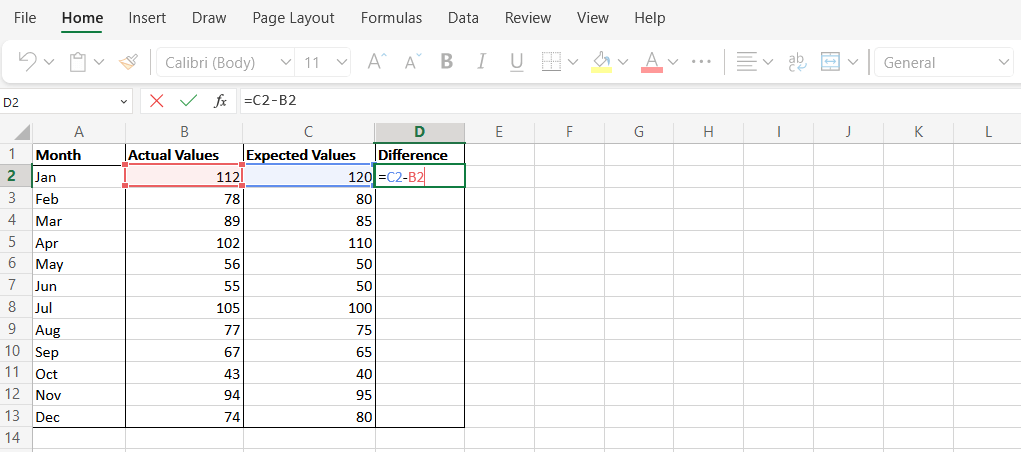
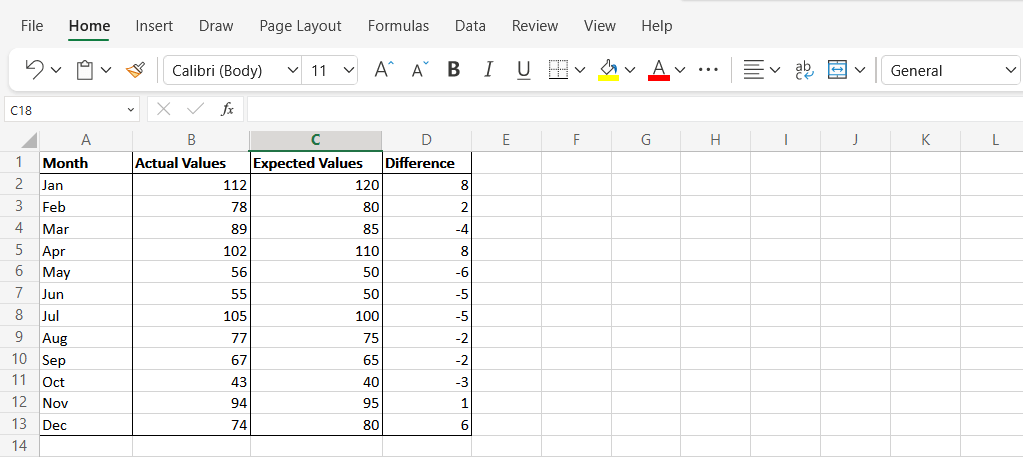
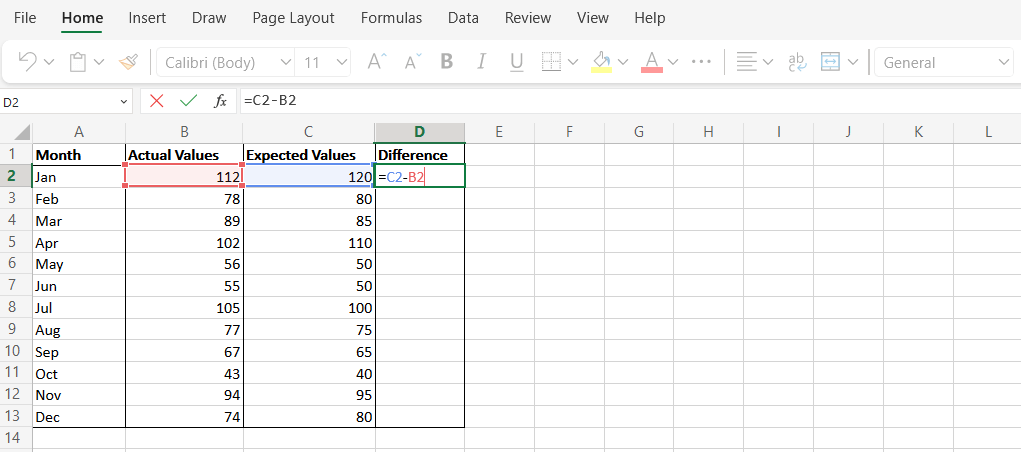
Calcule o MSE usando a função AVERAGE

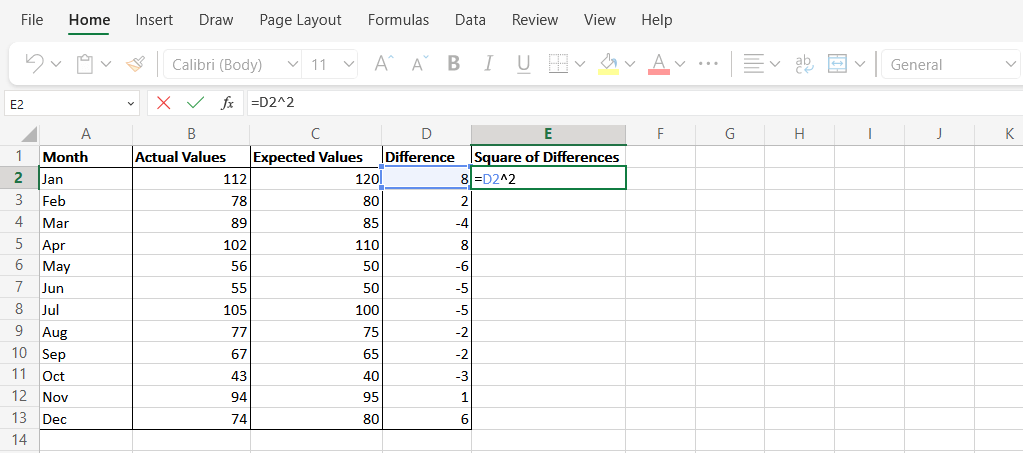
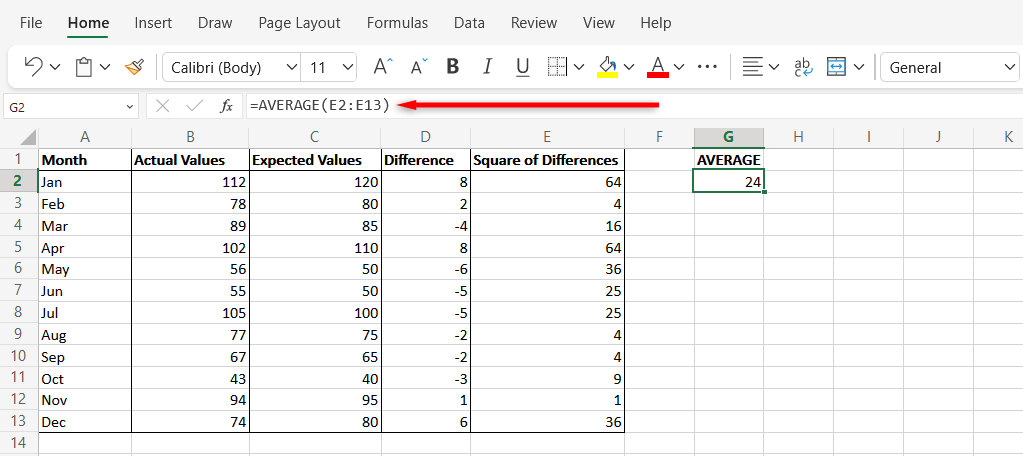
A função MÉDIA no MS Excel é usada para calcular a média de um intervalo de números. Este método retorna o mesmo resultado que a função SUMSQ, mas cada etapa é executada manualmente.

Execute as etapas 1 e 2 descritas no método SUMSQ. Isso retornará as diferenças entre os valores previstos e os dados reais.

Nomeie a Coluna E como “Quadrado das Diferenças” e use a fórmula “=D2^2” para calcular o quadrado da diferença de cada valor na Coluna D.

Selecione uma nova célula e calcule o valor médio da Coluna E. Isso retornará a média dos valores quadrados que você calculou anteriormente. Para fazer isso, digite “=AVERAGE(E2:E12)” e pressione Enter. Certifique-se de substituir as células pelas células usadas em planilha. O valor dos dados resultantes é o seu MSE.

Análise Estatística no Microsoft Excel

O Microsoft Excel é há muito tempo uma das ferramentas mais poderosas para análise de dados. Esperançosamente, com este tutorial, agora você pode usar o Excel para calcular o MSE facilmente. E, como são tão semelhantes, você poderá realizar os mesmos cálculos em Planilhas Google.

.

Postagens relacionadas: